Path-Level GNN-Based Retrievers

1.GNN-RAG: Graph Neural Retrieval for Large Language Model Reasoning

开源代码：https://github.com/cmavro/GNN-RAG

Motivation: 将GNN的推理能力和LLM的语言理解能力相结合用于知识图谱问答

Methodology：首先，GNN 对密集的 KG 子图进行推理，以检索给定问题的答案候选者。其次，提取 KG 中连接问题实体和答案候选项的最短路径以表示 KG 推理路径。提取的路径被文本化并作为使用 RAG 进行 LLM 推理的输入。在GNN-RAG 框架中，GNN 充当密集的子图推理器来提取有用的图信息，而 LLM 则利用其自然语言处理能力进行最终的 KGQA（知识图谱问答）

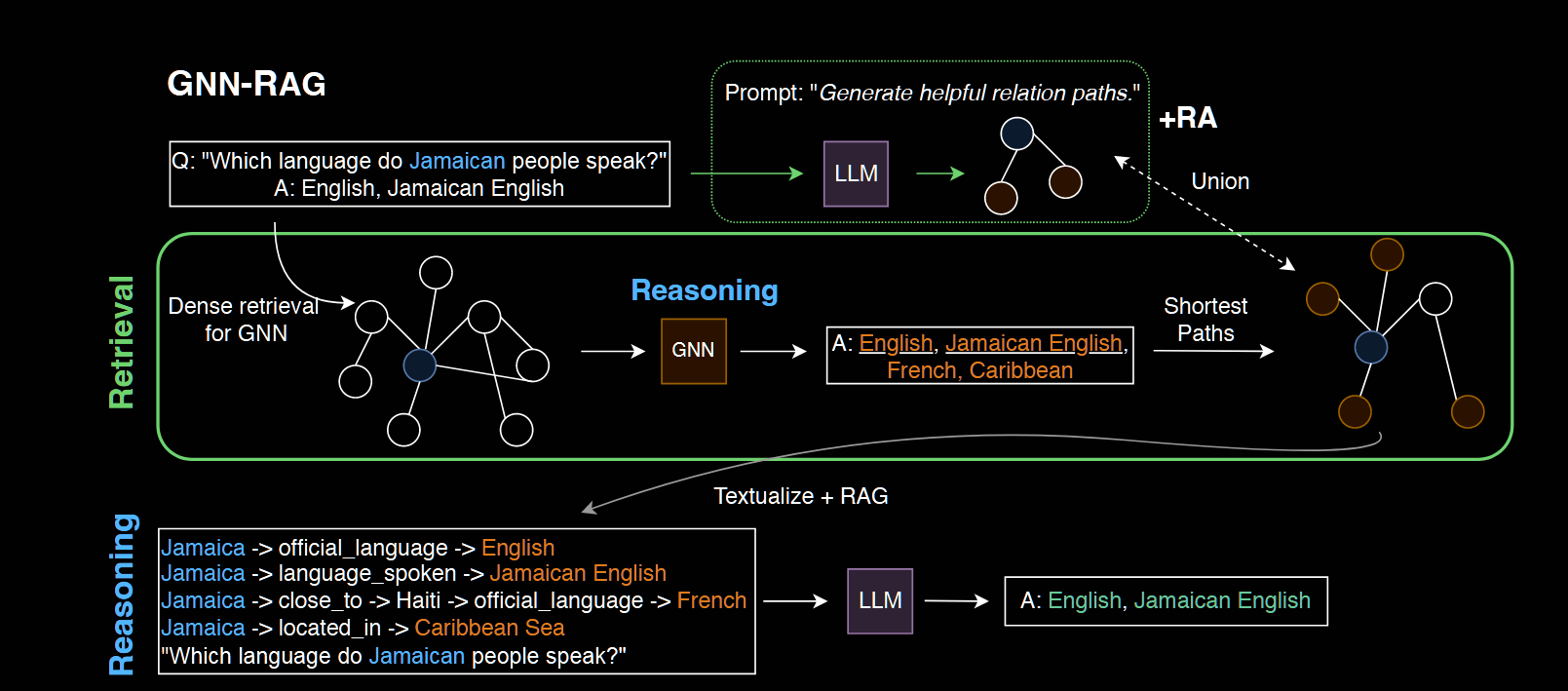
GNN的训练过程：将知识图谱问答KGQA任务视为节点分类，使用question-answer pairs训练集，将KG entities被分为answers和non-answers，

$h_v^{(l)}=\psi(h_v^{(l-1)}, \sum_{v’\in N_v}\omega(q,r)\cdot m_{vv’}^{(l)})$ Equ.1

其中函数$\omega(\cdot)$用来计算三元组(v,r,v’)中关系r和用户查询q之间的相关性。经过多跳传播后，所有节点根据最终表示被分为answer和non-answer两类。

此外，考虑到不同的GNN会产生不同的推理路径，如公式Equ.1所示，GNN的推理依赖于question-relation匹配函数$\omega(q,r)$，比较常用的设计方式为$\phi(q^{(k)}\odot r)$，其中$q^{(k)}$和$r$使用预训练语言模型来进行编码，$q^{(k)}=\gamma_k(LM(q)), r=\gamma_c(LM(r))$。

GNN的推理过程：具有最高概率分数的节点（例如，高于概率阈值）将作为候选答案返回，以及将问题实体与候选答案连接起来的最短路径（推理路径）。检索到的推理路径用作基于 LLM 的 RAG 的输入。

为了确保推理路径的多样性，这里作者并没有采用不同的GNN架构，而是使用了不同的LM通过更改$\omega$函数来引导单一的GNN获取不同的节点表示

LLM：没什么好说的，prompt-tuning

prompt: “Based on the reasoning paths, please answer the given question.\n Reasoning Paths: {Reasoning Paths} \n Question: {Question}”.

Reasoning paths 用语言描述为 “{question entity} → {relation} → {entity} → · · · → {relation} → {answer entity} \n”

2.Reasoning on Graphs: Faithful and Interpretable Large Language Model Reasoning

开源代码：https://github.com/RManLuo/reasoning-on-graphs

Motivation: 现有的基于 KG 的 LLM 推理方法仅将 KG 视为事实知识库，而忽视了其结构信息对推理的重要性。作者提出了一种称为图推理（TOG）的方法，并设计了一种规划检索推理框架，以实现忠实和可解释的推理

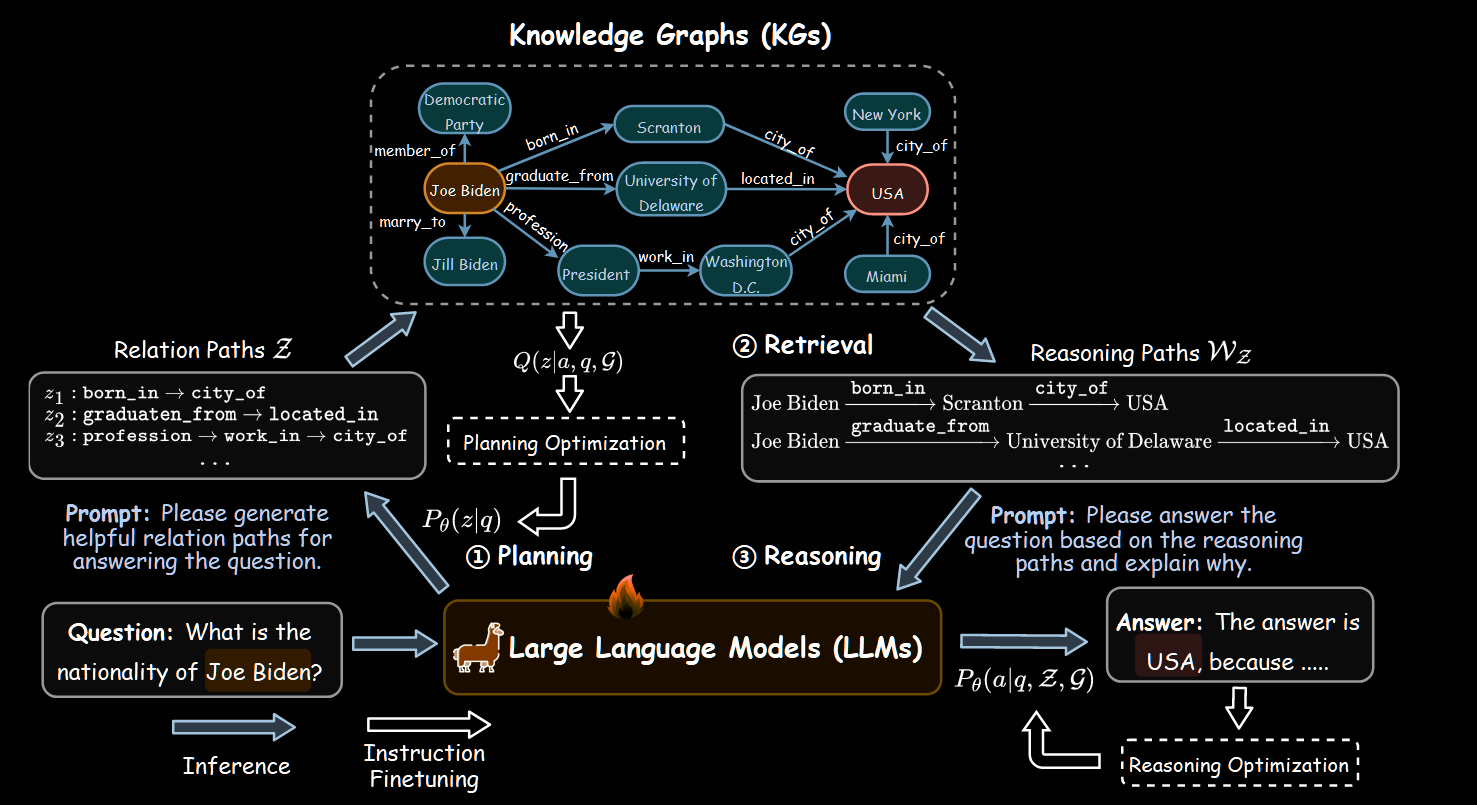
Methodology：RoG包含两个组件：（1）规划模块：基于用户查询生成关系路径作为KG的检索规划（2) 检索推理模块：根据规划模块的关系路径从KG中检索有效的推理路径。RoG通过两项任务进行优化：（1）规划优化，由于LLM对KG中包含的关系一无所知，该模块的训练目标是让LLM生成的关系路径尽可能近似于KG的有效路径。作者使用关系路径Q（z）的后验分布最小化KL发散来实现，该后验分布可以通过KGs中的有效关系路径来近似（2）检索-推理优化，给定问题q和作为规划z的关系路径，检索模块旨在从KG图G检索这个推理路径$W_z$。检索过程包括在G中查找路径，其从问题实体$e_q$开始并遵循关系路径z。采用一个约束的广度优先搜索（BFS）来检索来自KGs的推理路径$W_z$。实验中，所有检索的路径都用于推理。

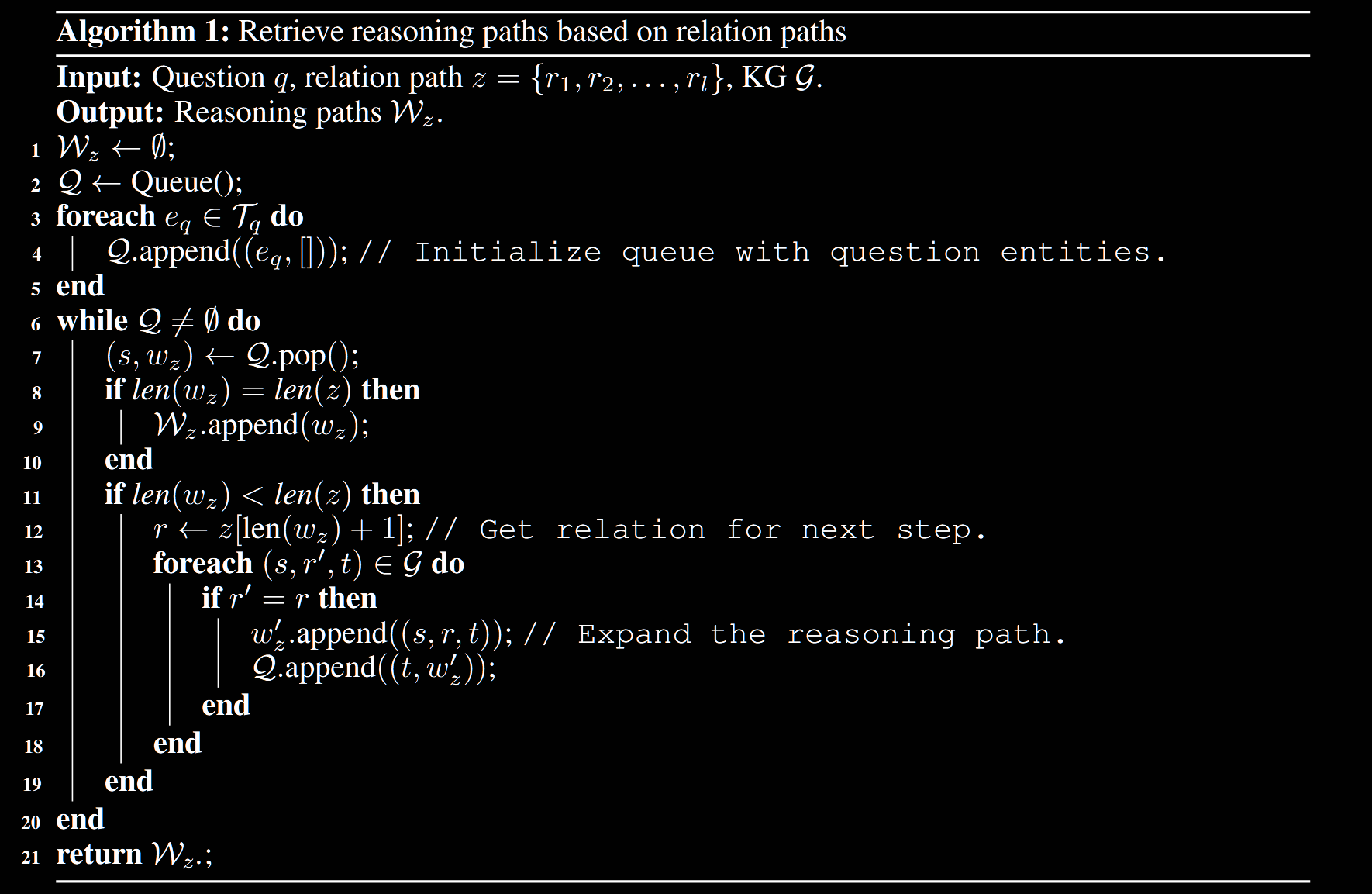
总结：LLM用来生成关系路径，在训练的过程中尽可能的去拟合KG中的真实路径。推理时首先让LLM根据用户查询生成路径规划，然后再KG查询对应的有效路径，作为检索结果，与用户查询一起作为LLM输入用户生成回复。