强化学习系列（一）:基础概念

三要素：

rewards, actions, states

马尔可夫奖励过程：

马尔可夫奖励过程可以表示为 $<S,P,R,\gamma>$，其中：

• $S$ 为状态集合；
• $P$ 为状态转移矩阵，$P_{ss’}=P[S_{t+1}=s’|S_t=s]$；
• $R$ 为奖励函数，$R_s=E[R_{t+1}|S_t=s]$；
• $\gamma$ 为折扣因子，$\gamma \in [0,1]$。

总折扣奖励：

回报（Return）$G_t$ 表示从时刻 $t$ 开始的总折扣奖励：
$$
G_t=R_{t+1}+\gamma R_{t+2}+…=\sum_{k=0}^\infty \gamma^k R_{t+k+1}
$$

• 状态价值函数：$v(s)=E[G_t|S_t=s]$
• 行为价值函数：$q(s,a)=E[G_t|S_t=s,A_t=a]$

Bellman 方程：

Bellman 方程表示状态价值函数的递归形式：
$$
v(s)=E[G_t|S_t=s]=E[R_{t+1}+\gamma R_{t+2}+…|S_t=s]=E[R_{t+1}+\gamma G_{t+1}|S_t=s]=E[R_{t+1}+\gamma v(S_{t+1})|S_t=s]
$$

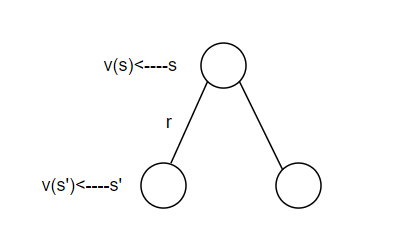
根据下方的状态价值迭代示意图，我们可以得到：
$$
v(s)=R_s + \gamma \sum_{s’ \in S}P_{ss’}v(s’)
$$

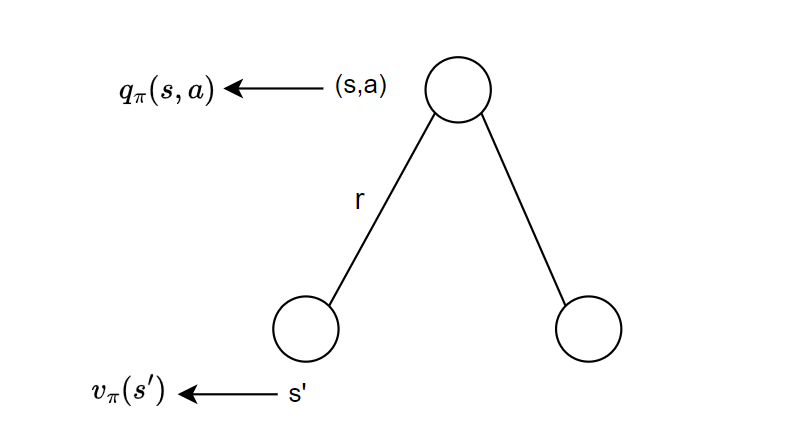
根据行为价值迭代示意图，可以得到：
$$
q(s,a)=R_s^a + \gamma \sum_{s’ \in S}P_{ss’}^a v(s’)
$$

马尔可夫决策过程：

马尔可夫决策过程（MDP）表示为 $<S,A,P,R,\gamma>$，其中：

• $S$ 是状态集合；
• $A$ 为动作集合；
• $P$ 为状态转移矩阵，$P_{ss’}^a=P[S_{t+1}=s’|S_t=s, A_t=a]$；
• $R$ 为奖励函数，$R_s^a=E[R_{t+1}|S_t=s, A_t=a]$。

状态的转移基于决策策略（policy）$\pi$ 所产生的动作，$\pi$ 用来基于当前状态给出下一步行动的规划：
$$
\pi(a|s)=P[A_t=a|S_t=s]
$$

价值函数：

由此，我们可以定义策略 $\pi$ 下的状态价值函数和行为价值函数：
$$
v_{\pi}(s)=E_{\pi}[G_t|S_t=s]
$$
$$
q_{\pi}(s,a)=E_{\pi}[G_t|S_t=s, A_t=a]
$$

使用即时奖励的形式，可以转换为：
$$
v_{\pi}(s)=E_{\pi}[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_t=s]
$$
$$
q_{\pi}(s,a)=E_{\pi}[R_{t+1}+\gamma q_{\pi}(S_{t+1},A_{t+1})|S_t=s, A_t=a]
$$

最优价值函数：

$$
v_*(s)=\max_{\pi}v_{\pi}(s)
$$
$$
q_*(s,a)=\max_{\pi}q_{\pi}(s,a)
$$

定理：如果对于任意的状态 $s$，都有 $v_{\pi}(s) \geq v_{\pi’}(s)$，则策略 $\pi$ 优于策略 $\pi’$。

Q&A：

Ques： 奖励是由状态变化产生的还是由行动产生的？
Ans： 奖励（Reward）通常是由 行动（Action） 产生的，而不是由状态变化直接产生的。在强化学习（RL）中，奖励的定义是智能体（Agent）在环境（Environment）中执行某个 动作 后得到的反馈，它表示智能体在采取该动作后获得的即时回报。状态变化是行为导致的结果。