强化学习系列(二):Model-free Prediction
写在前面: Prediction任务是用来在给定策略$\pi$的前提下,基于价值函数和奖励函数来评估该策略的好坏。Control任务用来对策略进行提升和改进。根据是否已知状态转移矩阵(MDP transition)分为Model-Based Prediction和Model-free Prediction
Model-Based Prediction&Control
1. Policy Iteration
策略迭代(Policy Iteration)是一种用于求解马尔可夫决策过程(MDP)的动态规划算法。它主要用于寻找最优策略,即在给定MDP的情况下,使得累计奖励最大的策略。
step: (1)策略评估(Policy Evaluation) Prediction Phase
在当前策略$\pi$下,计算所有状态s的状态函数$V^{\pi}(s)$, $V^{\pi}(s)=\sum_{a}\pi(a|s)[R_s^a +\gamma \sum_{s’}P_{ss’}^a V^\pi(s’)]$
(2) 策略改进(Policy Improvement) Control Phase
利用贪心策略来改进当前策略:$\pi’=greedy(\pi)$
具体来说,对于每个状态s,找到使得价值函数最大的动作a,从而得到最优策略$\pi*$
$\pi*(s)=argmax_a\sum_{s’}P_{ss’}^a[R_s^a + \gamma V^\pi(s’)]$
2. Value Iteration
价值迭代(Value Iteration)在更新状态时并不涉及策略$\pi$,它将根据最大的动作奖励与转移后的状态价值之和所对应的那个动作作为新的策略。即$V_{k+1}(s)=max_{a \in A}(R_s^a + \gamma \sum_{s’ \in S}P_{ss’}^a V_k(s’))$
下面给出Policy Iteration和Value Iteration的对比:
| 特点 | Value Iteration (值迭代) | Policy Iteration (策略迭代) |
|---|---|---|
| 思路 | 直接迭代更新值函数直到收敛,再提取最优策略 | 交替执行策略评估和策略改进,不断迭代优化策略 |
| 主要步骤 | 1. 更新值函数 → 2. 提取策略 | 1. 策略评估 → 2. 策略改进 → 3. 重复直到策略收敛 |
| 收敛条件 | 值函数变化足够小 ( | V_{k+1} - V_k |
| 策略提取时机 | 最后一步提取最优策略 | 每轮策略改进都会更新策略 |
| 计算量 | 更新每个状态时都考虑所有动作(计算量大但收敛快) | 每次完整评估策略再改进策略,可能需要多次评估,但改进次数较少 |
| 策略更新 | 从值函数提取策略(离线策略) | 每次改进立即生成新策略(在线策略) |
Model-Free Prediction
1. Monte-Carlo Reinforcement Learning
特点:no bootstrapping(bootstrapping是指用现有的估计值来更新当前的估计值),即不依赖未来状态的估计值,每次只用真实的经验回报来更新策略。
bootstrapping(Q-learning、SARSA): 更新值依赖于未来状态的估计值
$Q(s,a) \leftarrow Q(s,a) + \alpha(r + \gamma Q(s’,a’) -Q(s,a))$ 这里的Q(s’,a’)就是对未来的估计值
no bootstrapping(Monte Carlo): 完全基于真实的完整回报𝐺更新,不依赖未来状态的估计
$Q(s,a) \leftarrow Q(s,a) + \alpha(G-Q(s,a))$ 其中$G=\sum_{t’=t}^T \gamma^{t’-t}r_{t’}$
| 特性 | No Bootstrapping | Bootstrapping |
|---|---|---|
| 代表算法 | Monte Carlo, REINFORCE | Q-learning, SARSA, TD(0) |
| 更新依赖 | 完整回报 | 未来状态的估计值 |
| 误差来源 | 高方差 | 有偏差(因依赖估计值) |
| 收敛速度 | 慢(方差大、数据需求多) | 快(但可能收敛到次优解) |
| 实时性 | 必须等完整轨迹结束才更新 | 可以在线更新,每一步都能调整 |
step: 为了估计状态s,每一次采样路径经过状态s时,$N(s) \leftarrow N(s)+1$,同时增加累积回报 $S(s) \leftarrow S(s) + G_t$。最终,采用平均估计的方式得到状态价值V(s)=S(s)/N(s)。接下来更新策略$V(s) \leftarrow V_{\pi}(s)$,直到$N(s) \leftarrow \infty$
根据$\mu_k = \frac{1}{k}\sum_{j=1}^k x_j=\mu_{k-1}+\frac{1}{k}(x_k-\mu_{k-1})$
$V(S_t) \leftarrow V(S_t) + \frac{1}{N(S_t)}(G_t -V(S_t))$
通常情况下,我们将这里的$\frac{1}{N(S_t)}$替换为折损因子\alpha,即$V(S_t) \leftarrow V(S_t) + \alpha(G_t -V(S_t))$
2. Temporal Difference Learning
利用Bellman方程的方式来泛化估计$G_t$,即$V(S_t) \leftarrow V(S_t) + \alpha(R_{t+1} + \gamma V(S_{t+1})-V(S_t))$
其中$R_{t+1} + \gamma V(S_{t+1})$为TD Target, $\delta_t=R_{t+1} + \gamma V(S_{t+1}) - V(S_t)$为TD Error
| 特性 | TD Learning | Monte Carlo (MC) |
|---|---|---|
| 更新时机 | 每一步更新(在线学习) | 完整轨迹结束后再更新 |
| 回报估计 | 依赖当前经验 + 未来估计值(bootstrapping) | 依赖完整回报(no bootstrapping) |
| 偏差 vs. 方差 | 有偏但方差小(因为估计依赖未来状态的值) | 无偏但方差大(因为回报波动大) |
| 收敛速度 | 快,能更快调整值函数 | 慢,因为要等待完整回报 |
| 适用场景 | 适用于连续或在线任务 | 适用于回合式任务(如游戏) |
3. N-Step Prediction(TD Learning的变体)
将TD target设定为未来n步的奖励和转移状态期望,相当于TD和MC的折中,迭代n步再更新
Consider the following n-step returns for n=1,2…,\infty
n=1 (TD) $G_t^{(1)}=R_{t+1}+\gamma V(S_{t+1})$
n=2 (2-Step) $G_t^{(2)}=R_{t+1}+\gamma R_{t+2} + \gamma^2 V(S_{t+2})$
… … …
n=\infty (MC) $G_t^\infty=R_{t+1}+\gamma R_{t+2} + … + \gamma^{T-1}R_T$
因此,对于n-step temporal-difference learning: $V(S_t) \leftarrow V(S_t) + \alpha(G_t^{(n)}-V(S_t))$
4. Lamda Return(N-Step Prediction的变体)
考虑了短步回报和长步回报的不同收益: $G_t^\lambda= (1-\lambda)\sum_{n=1}^\infty \lambda^{n-1}G_t^{(n)}$
$V(S_t) \leftarrow V(S_t) + \alpha (G_t^\lambda- V(S_t))$
λ 越小,更依赖当前的 TD 估计,快速调整但可能抖动大; λ 越大,更依赖长时间的回报,稳定但更新慢
总结
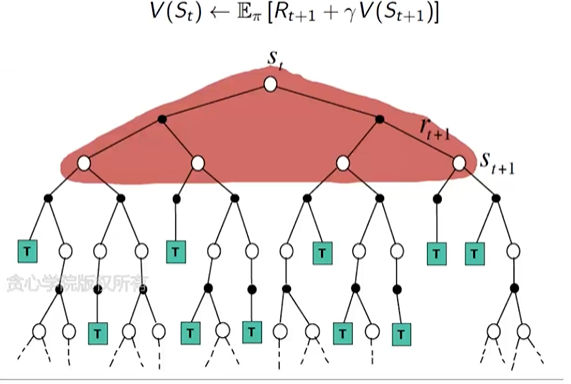
Monte Carlo Backup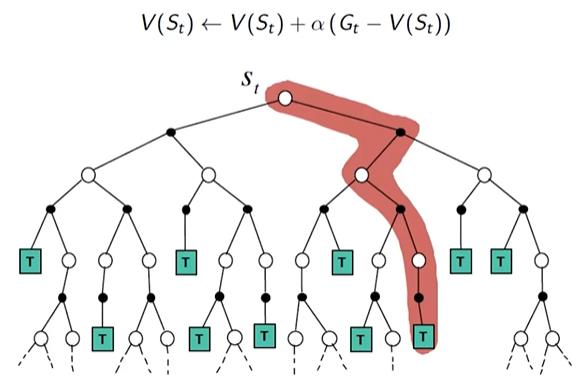
Temporal-Difference Backup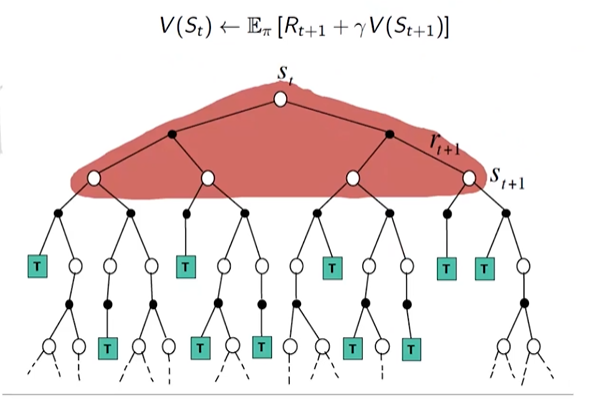
Dynamic Programming Backup(Policy/Value Iteration)