强化学习系列(四):DQN算法
写在前面:前面讲解了在On-Policy和Off-Policy环境下如何进行策略提升的几种常用方法,但是在实际应用场景中,state的数量可能是非常庞大的,为了存储每个state-action pair所需要的lookup-table所需要的空间会很庞大,无法通过遍历的方式去evaluate每个state-action pair。这就需要我们考虑如何对Q,V进行建模,通过函数逼近的方法估计连续空间下的state value
1. Value Approximation
Target: 寻找到合适的参数w使得mse loss尽可能的小 $J(w)=E_\pi[(v_\pi(S)-\hat{v}(S,w))^2]$
通过梯度下降来更新w: $\Delta w=-\frac{1}{2}\alpha \nabla_w J(w)=\alpha(v_\pi(S)-\hat{v}(S,w))\nabla_w\hat{v}(S_t,w)$
使用特征向量表示state $x(S)=(x_1(S)…x_n(S))$
$\hat{v}(S_t,w)$可以通过线性加权得到,即$\hat{v}(S,w)=x(S)^Tw=\sum_{j=1}^n x_j(S)w_j$
于是我们便有:$\Delta w=\alpha(v_\pi(S)-\hat{v}(S_t,w))x(S)$
现在思考一个问题,我们如何得到$v_\pi(S)$的真实表示?依然是采用MC/TD等方法进行泛化估计
MC: $\Delta w=\alpha(G_t-\hat{v}(S,w))\nabla_w\hat{v}(S_t,w)$
TD(0): $\Delta w=\alpha(R_{t+1}+\gamma\hat{v}(S_{t+1},w)-\hat{v}(S_t,w))\nabla_w\hat{v}(S_t,w)$
2. Replay Buffer
replay buffer是一个 存储智能体交互经验 的数据结构(通常是一个队列或数组),用来保存智能体与环境交互的轨迹样本:$(S_t, A_t, S_{t+1}, A_{t+1}, done)$
✅ 打破时间相关性 (Break Correlation)
强化学习中的数据是按时间顺序生成的,彼此高度相关。Replay Buffer让我们从过去的经验中随机采样,打乱数据顺序,降低相关性,提升训练稳定性。
✅ 提高数据利用率 (Improve Data Efficiency)
每次交互生成的数据如果只用一次就丢掉,效率太低了。Replay Buffer让数据能被多次复用,大大提高训练效率。
✅ 平滑训练 (Smooth Training)
缓冲区里的经验包括成功和失败的多种场景,防止模型被最近的几次失败经验“误导”得太严重。
✅ 支持 Off-Policy 学习
DQN 是 Off-Policy 算法,目标策略是贪婪策略,行为策略是ϵ-greedy。Replay Buffer让我们从过去的经验中训练,不必跟当前行为策略严格匹配。
3. DQN算法
DQN算法是结合了Q-Learning和深度神经网络的强化学习算法。它用深度神经网络替代传统的Q表格,近似的学习Q值函数:$Q(s,a;\theta) \approx Q*(s,a)$
下面对该算法进行介绍:
(1)经验回放(Experience Replay)
在传统Q-Learning中,每次训练都用最新的数据更新Q值,可能导致网络过拟合最近的经验,收敛不稳定。
DQN引入经验回放机制,将每次经历 (s, a, r, s’) 保存到回放缓冲池(Replay Buffer),每次训练时随机采样一批数据进行训练。
(2)目标网络(Target Network)
DQN使用在线网络和目标网络两个网络,前者用于实时更新,输出$Q(s,a;\theta)$;后者每隔一段时间赋值在线网络参数$\theta$到目标网络$\theta’$,输出$Q(s’,a’;\theta’)$
目标网络的Q值用作训练的目标: $Loss=(r + \gamma max_{a’}Q(s’,a’;\theta’)-Q(s,a;\theta))^2$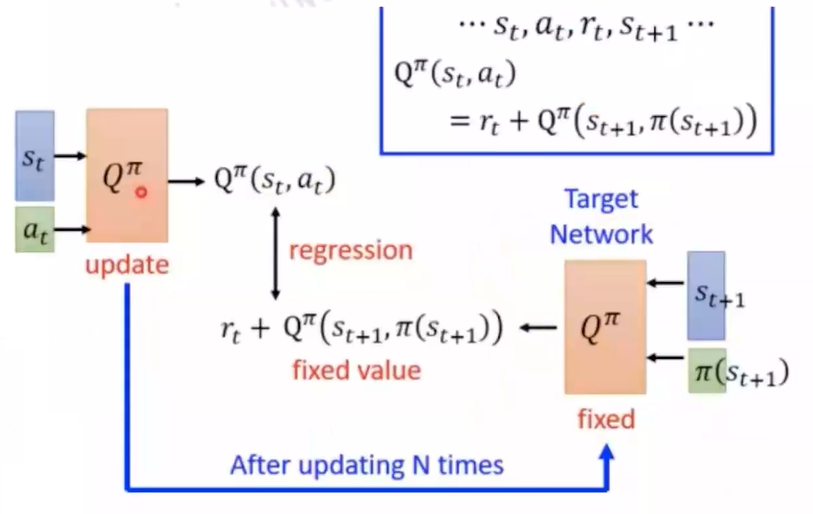
(3)使用Epsilon Greedy策略在探索与利用之间做权衡
下面给出DQN算法的伪代码:
Ques: DQN网络如何实现端到端的学习
Ans: 中间层是常规的卷积网络用来学习state表征,输出层通过映射到一个output空间,定义每个维度代表一个value
4. DQN算法的延伸
Double DQN
DQN算法存在的问题:使用同一个网络既选择动作又评估价值,可能会导致over estimate的问题
改进方案:$Q(s_t,a_t) \leftarrow r_t + Q’(s_{t+1}, argmax_a Q(s_{t+1},a))$ 内层的Q用来选择action,外层的Q用来评估价值
Dueling DQN
DQN算法存在的问题:在很多状态下,动作的价值差别不大。比如:游戏中站在原地等待 vs 随便走一步 这种情况下,DQN仍然必须给每个动作单独估计 Q 值,浪费了大量学习能力,导致训练效率下降。
Dueling DQN的核心思想:将Q值分成两部分,状态值函数 V(s):描述当前状态本身的“好坏” 优势函数 A(s, a):描述某个具体动作比其他动作好多少
于是,我们便有:$Q(s,a)=V(s)+A(s,a)$
优点:状态价值主导训练,不用每次都算所有动作;更高效地学习,尤其在动作多、动作差别小的场景;收敛更快,性能更好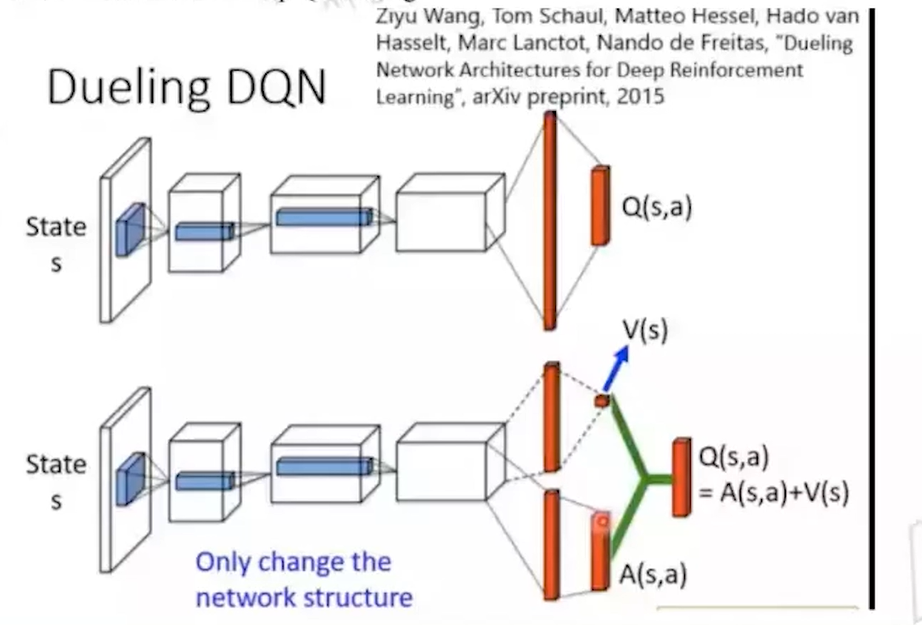
Batch-Constraint DQN(BCQ)
DQN算法存在的外推误差(extrapolation error)问题:Q网络在没见过的state-action pair上会over estimate Q值
问题的根源在于:有限的数据集:训练数据无法覆盖所有可能的状态-动作对。目标网络延迟更新:目标 Q 值用的是旧网络(延迟更新),可能不准确。最大化操作带来的偏差:maxQ 倾向于选更高估的值。
核心思想:尽可能让agent action和batch中sample action产生的结果相近,即约束策略不要偏离已收集的数据分布,同时最大化回报
下面给出BCQ算法的伪代码:
可以看到,在行为选择时,除了考虑高Q值以外,我们还希望它能够接近数据分布的action,伪代码的第5行中我们通过设定阈值的方式筛选掉了一些发生概率较低的action
Distributional Q-function
DQN算法存在的问题:在DQN中,我们学的是Q值的期望,$Q(s,a)=E[R(s,a)]$ 但问题是,期望值无法描述奖励的不确定性和波动。也就是说,DQN 只学到了平均回报,没学到“回报的分布情况”。
👉 举个例子:假设有两个动作$a_1$和$a_2$,它们的期望回报都是 10。$a_1$的回报是 [10, 10, 10],非常稳定。$a_2$的回报是 [0, 10, 20],波动很大。传统 DQN 认为它俩一样好,但显然$a_1$更可靠
核心观点:学习回报的“完整分布” $Q(s,a)=E[Z(s,a)]$ 这里的Z(s,a)为一个概率分布
step:定义回报范围$[v_min,v_max]$,划分为n个小区间;学习每个bin的概率$p_i$,形成一个回报的离散分布;训练目标变成让网络预测整个分布,而不是单一Q值