RLHF(二)：偏好数据采集

ORM 和 PRM

ORM：结果奖励模型，是不管推理有多少步，对完整的生成结果进行一次打分，是一个反馈更稀疏的奖励模型
PRM：过程奖励模型，是在生成过程中，分步骤，对每一步进行打分，是更细粒度的奖励模型

使用PRM可以在post-training和inference两个阶段提升模型的推理性能：

• Post-Training阶段：在偏好对齐阶段，通过在RL过程中增加PRM，对采样的结果按步骤输出奖励值，为模型提供更精细的监督信号，来指导策略模型优化，提升模型按步推理的能力
• Inference阶段：对于一个训练好的PRM，可以在inference阶段筛选优质生成结果。

MCTS 蒙特卡洛树搜索

MCTS是强化学习领域提出的方法，通过采样方式预估当前动作或状态的价值。具体操作步骤：使用已有的策略与环境做仿真交互，进行多次rollout采样，最终构成了一个从当前节点出发的一颗Tree（每个rollout表示从当前节点到最终结束状态的多次与环境仿真交互的过程）。这颗Tree的所有叶子节点都是结束状态，结束状态是可以通过定义规则进行量化收益的。当Tree的叶子结点有了奖励值，就可通过反向传播，计算每个中间节点的奖励值，最终计算出整个Tree所有节点的奖励值。MCTS一次rollout包括：sample，expand，simulate，backprop四个步骤。

• Sample(采样)：选择一个未被探索的节点，在Reasoning Model中的节点表示一个带有特定标签的推理步骤（如：planning 节点，reflection节点等）。初始情况，Tree只有一个表示原始查询的节点
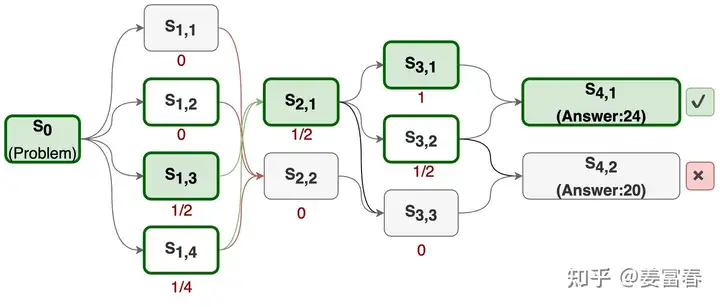
• Expand(扩展)：从未被选择的节点出发，展开所有可能的子节点，如下图中从$S_0$到$S_{1,1}, S_{1,2}, S_{1,3}, S_{1,4}$的过程。对于文本生成模型，不可能穷举所有子节点(next token)，因此需要设置一个最大生活次数，即最大子节点个数。
• Simulate(模拟)：从展开的子节点中，随机选择一个节点，再展开它的子节点，重复进行expand过程。直到达到叶子结点。该迭代过程需要控制搜索树的最大深度N
• Backprop(回传)：通过多次模拟我们得到了一个从根节点到叶子结点的Tree，如下图所示。通过计算(从当前节点出发到正确答案的路径数)/(从当前节点出发的总路径数)的比值作为节点的奖励值。

使用MCTS也可以在post-training和inference两个节点提升模型的推理性能：

• Post-Training阶段: 对于每个problem 通过上述方法构造一个搜索Tree，然后进行Tree的游走遍历采样，再用采样的样本SFT或RL训练模型。
• Inference阶段：在推理阶段，也是对一个problem探索多节点构造一棵搜索树，对于到达正确答案的路径，根据节点路径的置信度打分，贪心选取最优路径作为最终的推理结果。

分而治之：OmegaPRM

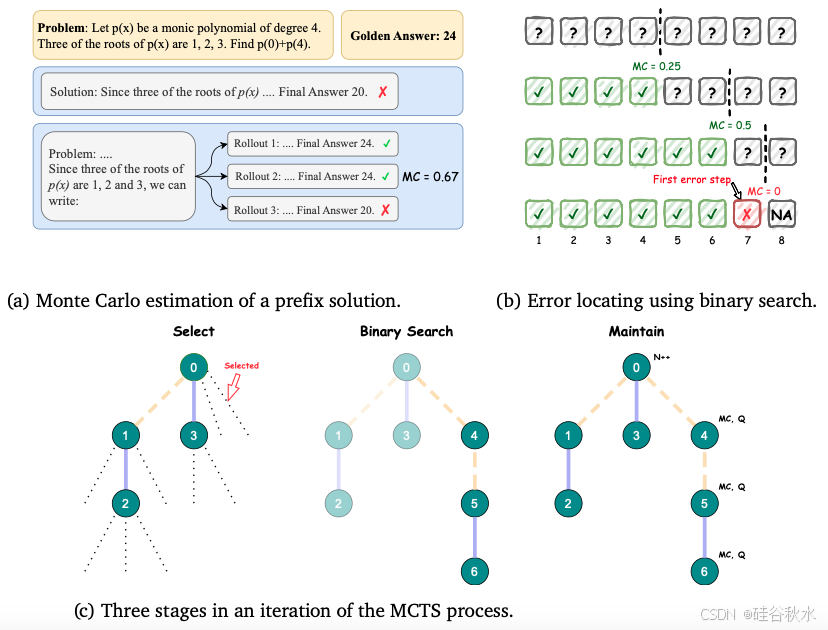
由于MCTS和PRM方法的规模化成本过高，为了更高效的收集高质量的过程监督数据，OmegaPRM算法通过二分搜索快速识别思维链CoT中的第一个错误，并平衡正反例，从而确保效率和质量。

OmegaPRM的搜索树如下图所示，树中的每个节点都表示部分思维链解决方案的状态，其中包含信息，如推出的准确性和其他统计数据。每条边都表示从上一个状态开始的一个动作，即推理步骤。黄色边是正确的步骤，蓝色边是错误的步骤。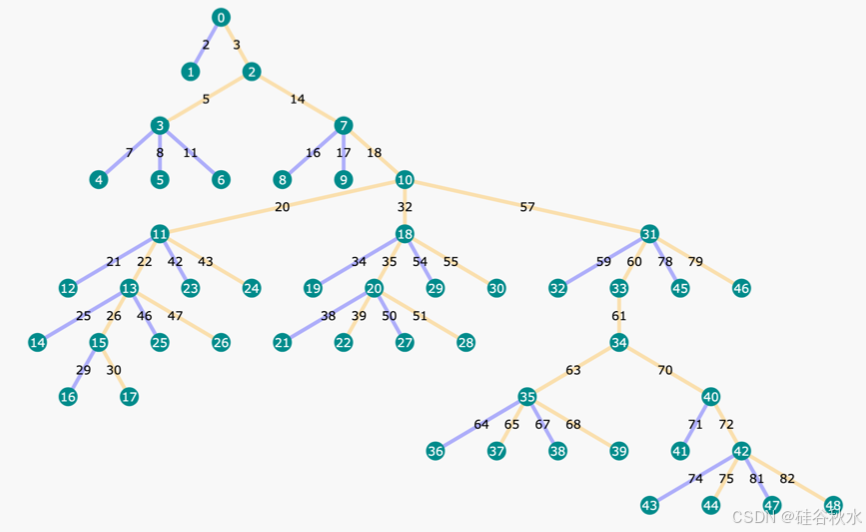

搜索算法的具体实现如下：建立了一个完成者策略，该策略可以采用问题 𝑞 和一个由前 𝑡 步骤 $𝑥_{1:𝑡}$ 组成的前缀解决方案，并输出后续步骤的完成情况（在强化学习中通常称为rollout），直到得出最终答案。对于解决方案的任何步骤，完成者策略可用于从该步骤中随机抽取 𝑘 个 rollout。将这些 rollout 的最终答案与正确答案进行比较，提供与 𝑘 个 rollout 相对应的 𝑘 个答案正确性标签。随后，计算第 𝑡 步中正确 rollout 占总 rollout 的比率，公式1 展示了估计前缀步骤 $𝑥_{1:𝑡}$ “正确性水平”的方法。只要在逻辑推理场景中任何一个推出是正确的，𝑥1:𝑡 就应该被视为正确的。为了优化注释效率，OmegaPRM采用二分搜索的蒙特卡洛估计，如下图所示。
$c_t = MontoCarlo(q,x_{1:t}) = \frac{Num(\text{correct rollouts from t-th step})}{Num(\text{total rollouts from t-th step})}$