时间序列分解

1. 时间序列分解

时间序列由两个组成要素构成：1、第一个要素是时间要素；2、第二个要素是数值要素。时间序列根据时间和数值性质的不同，可以分为时期时间序列和时点时间序列。

一般情况下，时间序列的数值变化规律有以下四种：长期变动趋势、季节变动规律、周期变动规律和不规则变动。

长期趋势： 长期趋势指的是统计指标在相当长的一段时间内，受到长期趋势影响因素的影响，表现出持续上升或持续下降的趋势，通常用字母T表示

季节变动： 由于季节的转变使得指标数值发生周期性变动，一般以月、季、周为时间单位，不能以年作单位，通常用S表示

循环变动： 循环变动通常以若干年为周期，在曲线图上表现为波浪式的周期变动。这种周期变动的特征变现为增加和减少交替出现，通常用C表示

不规则变动： 由某些随机因素导致的数值变化，这些因素的作用是不可预知和没有规律性的，因此对数值的变化影响变形为不规则变动， 通常用I表示

四种变动与指标数值最终变动的关系可能是叠加关系，也可能是乘积关系。

叠加模型：$Y=T+S+C+I$
乘积模型：$Y=TSC*I$

反映在具体的时间序列图上，如果随着时间的推移，序列的季节波动变得越来越大，则反映各种变动之间的关系发生变化，建议使用乘积模型；反之，如果时间序列图的波动保持恒定，则可以直接使用叠加模型。

2. 基于移动平均法的长期趋势分析

移动平均法的实质是通过对变量值进行平均的方法，对原来的时间数列进行修匀，以消除季节变动、不规则变动等其他因素对数列产生的影响。移动平均法又可以分为简单移动平均、加权移动平均和指数平滑三种形式。注意：移动平均法一般只适用于具有直线趋势的时间数列。

（1）简单移动平均：
步骤：1. 确定移动的项数k，即每次平均时所包含的变量值的个数 2. 从时间数列的第一个变量值开始，每次向后移动一项，分别计算出k个数值的序时平均数 3. 将计算出来的每个移动平均数的数值与它所对应的时间对应排列，编制成一个新的时间数列

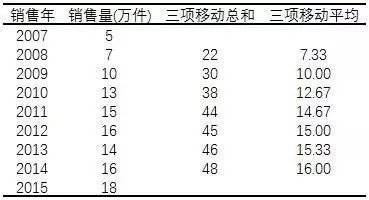
应用移动平均法进行趋势分析有几个注意点：

1、应合理选择移动项数。移动项数越多，修匀效果越好，但新时间数列项数越少，不利于进行长期趋势分析；反之，移动项数越少新数列项数多，修匀效果不好。所以应根据所研究对象的具体特点，来确定移动的项数。如果原数列指标数值有周期性变化，应以周期的长度作为移动的项数。例如，季度资料作四项移动平均，月资料作十二项移动平均，这样可以消除周期性的季节影响。

2、利用平均法进行长期趋势分析时要有足够的资料，否则不能如实放映现象固有的变化趋势，这也是进行长期趋势分析的前提条件。

3、移动平均后的数值要与原数列时间对应。如果是奇数项，平均数落在中间项上，例如，进行3项移动平均，移动平均数落在第2项（(k+1)/2）；如果是偶数项，平均数落在两项中间，还应进行项数为2的移动平均

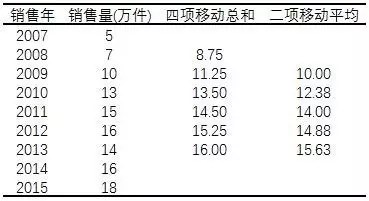
（2）加权移动平均法

简单移动平均法每个观测值都用相同的权数，即假定过去各期的资料对预测期的影响程度相同。但在加权移动平均中，每个观测值被赋予相应的权重。例如，在大多数情况下，越近的资料应该有最大的权重，而较远的资料的权重较低。

示例：采用三项加权移动平均，最近时期观测值的权数为最远时期观测值的3倍，中间时期观测值的权数为最远时期的2倍

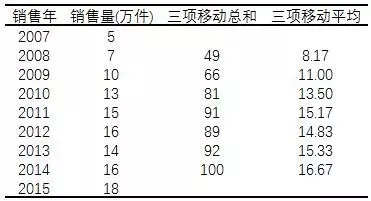
（3）指数平滑法

指数平滑法是加权移动平均法的一种特殊情形。只选择一个权数，即最近时期观测值的权数，其它时期数据值的权数可以自动推算出来，观测值离预测时期越远，它的权数就越小。模型定义如下：
$\hat{Y}_{i+1} = \alpha Y_i + (1-\alpha) \hat{Y}_i$ 其中$\alpha$为平滑系数，$1-\alpha$为阻尼系数，$Y_i$为实际值，$\hat{Y}_i$为预测值

现在根据包含三个时期资料的时间数列Y1，Y2和Y3，来说明任何时期指数平滑法的预测值，同样也是时间数列以前所有时期实际值的一个加权平均数。

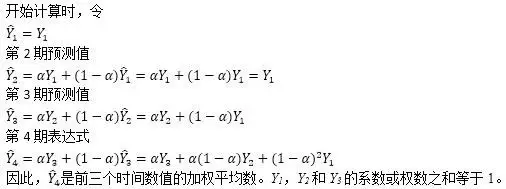
经验判断法：

1、当时间序列呈现较稳定的水平趋势时，应选较小的α值，一般可在0.05~0.20之间取值；

2、当时间序列有波动，但长期趋势变化不大时，可选稍大的α值，常在0.1~0.4之间取值；

3、当时间序列波动很大，长期趋势变化幅度较大，呈现明显且迅速的上升或下降趋势时，宜选择较大的α值，如可在0.6~0.8间选值，以使预测模型灵敏度高些，能迅速跟上数据的变化；

4、当是上升（或下降）的发展趋势类型，α应取较大的值，在0.6~1之间。

3. 季节变动分析

（1）同期平均法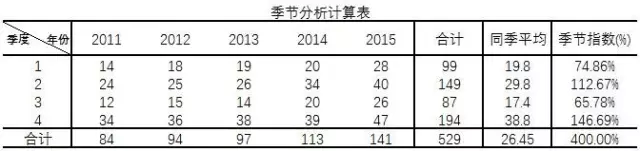

缺点：但是这种方法计算的结果误差较大，因为这种方法没有考虑到长期趋势变化的影响

（2）长期趋势剔除法

先确定出各期的趋势值，然后再从观测值中扣除趋势值，从而测定季节指数。

示例：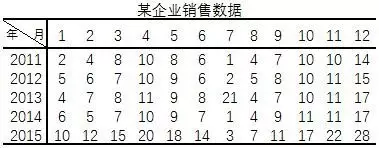

将上面的数据做散点图：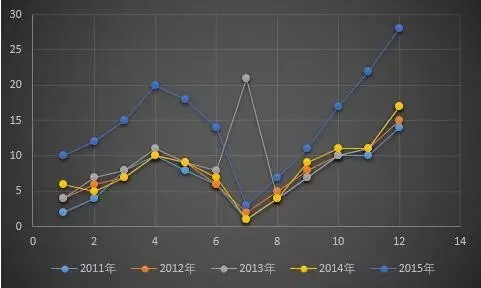

从图上看，虽然每年的数据起伏波动较大，但是这种波动具有明显的规律性，即每年第一季度和第三季度的销售量相对较低，而第二季度和第四季度的销售量相对较高，这说明销售量的变化受季节变动的影响。同时随着时间的推移，销售量又逐年增加，这说明销售量的变化也受长期趋势的影响。因而，为了准确的确定季节指数，就需要剔除长期趋势对销售量的影响，即应该采用长期趋势剔除法。分析步骤如下：

1. 对给定的数列先进行四项（以季为单位的资料）或十二项（以月为单位）的移动平均，从而消除不规则变动（I）和季节变动（S）影响，得到趋势分量（T）和循环分量（C）。
   
   
   

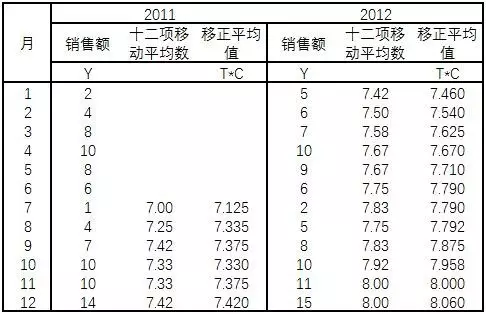
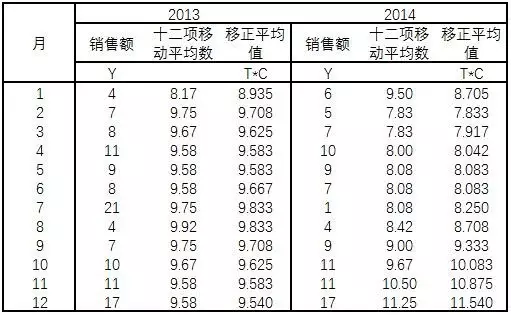
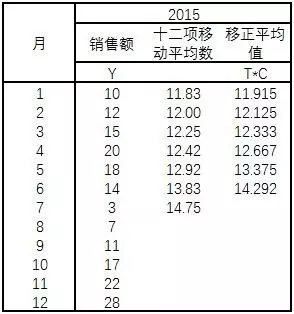
2. 从原数列中扣除长期趋势和循环分量影响，分离出季节分量和不规则分量(SI)： $SI=Y/T*C$

例如：2011年1月数据，SI=Y/TC=1/7.125=14.04%；

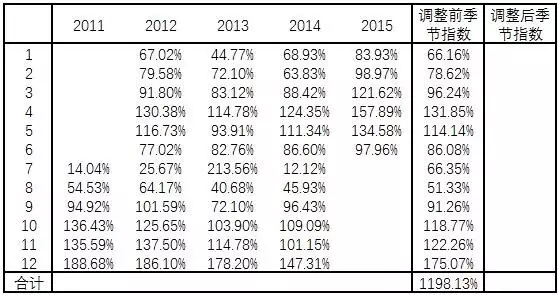
3、从季节分量和不规则分量（S*I）中应用平均法消除由于偶然因素引起的不规则变动的影响，分离出季节指数（S）。

调整前季节指数：每年同一个月的均值，例如2011年1月，(67.02%+44.77%+68.93%+83.93%)/4=66.16%，即将季节分量和不规则分量经过简单平均消除不规则变动的影响后，分离出调整前季节分量。

调整后季节指数：从理论上说，如果没有季节因素影响，各期季节指数都应该是100%，12个月的季节指数之和应为1200%，实际为1198.13%，所以调整系数为：调整系数=1200%/1198.13%=1.00016；然后用调整系数乘调整前季节指数得到调整后指数。

计算结果如下：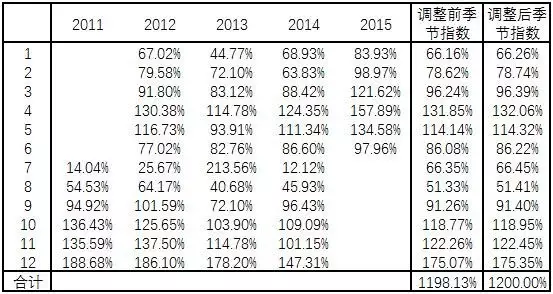

4. 循环变动分析

循环变动是指一年以上的周期内，时间数列沿着长期趋势直线上下波动变化。循环变动分析过程如下：

1、首先将原始数据（按月、季、天等）构成的时间数列，调整为以年为单位的时间数列。因为在影响时间数列的四种因素中，季节变动是一年内的有规律变化，不影响其它年份，所以使用以年为周期的时间数列消除了季节变动影响，只反映长期趋势、循环变动和不规则变动的影响。

2、利用趋势方程确定长期趋势T。

3、不规则变动假定为随机变量，在一段时间上的变化总量趋于0.

4、确定循环变动C。

循环变动可以用趋势百分数表示，公式如下：

*趋势百分数(C)=实际观测值(Y)/长期趋势值(T)100%

示例:
某公司近9年的销售情况如下表：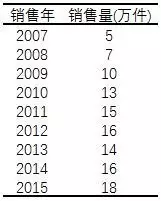

用最小二乘法，计算过程可回顾：长期趋势分析，趋势方程为：T=12.67+1.5X，其中T为长期趋势值。

可列出循环变动计算表：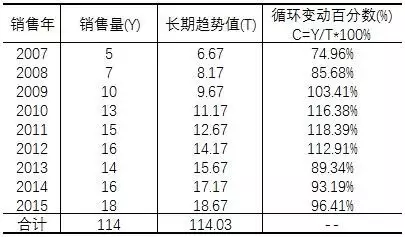

可以看出，实际值围绕长期趋势直线波动幅度在74.96%至118.39%之间。用循环变动百分数可以描述过去循环变动的变化情况。但是由于影响循环变动的因素难以预料，所以不能进行未来推断。